 |
Open CASCADE Technology
7.7.0
|
|
 |
Open CASCADE Technology
7.7.0
|
|
This manual explains how to use Open CASCADE Technology (OCCT) Foundation Classes. It provides basic documentation on foundation classes.
Foundation Classes provide a variety of general-purpose services such as automated dynamic memory management (manipulation of objects by handle), collections, exception handling, genericity by down-casting and plug-in creation.
Foundation Classes include the following:
Root classes are the basic data types and classes on which all the other classes are built. They provide:
Strings are classes that handle dynamically sized sequences of characters based on UTF-8 and UTF-16 encodings. Strings may also be manipulated by handles, and consequently be shared. Strings are implemented in the TCollection package.
Collections are the classes that handle dynamically sized aggregates of data. Collection classes are generic and rely on C++ templates.
Collections include a wide range of generic classes such as run-time sized arrays, lists, stacks, queues, sets and hash maps. Collections are implemented in the TCollection and NCollection packages.
The TColStd package provides frequently used instantiations of generic classes from the TCollection package with objects from the Standard package or strings from the TCollection package.
These classes provide commonly used mathematical algorithms and basic calculations (addition, multiplication, transposition, inversion, etc.) involving vectors and matrices.
Open CASCADE Technology primitive geometric types are a STEP-compliant implementation of basic geometric and algebraic entities. They provide:
Open CASCADE Technology common math algorithms provide a C++ implementation of the most frequently used mathematical algorithms. These include:
A hierarchy of commonly used exception classes is provided, all based on class Standard_Failure, the root of exceptions. Exceptions describe exceptional situations, which can arise during the execution of a function. With the raising of an exception, the normal course of program execution is abandoned. The execution of actions in response to this situation is called the treatment of the exception.
These are various classes supporting date and time information.
Foundation Classes also include implementation of several low-level services that facilitate the creation of customizable and user-friendly applications with Open CASCADE Technology. These include:
This chapter deals with basic services such as library organization, persistence, data types, memory management, programming with handles, exception handling, genericity by downcasting and plug-in creation.
This chapter introduces some basic concepts, which are used not only in Foundation Classes, but throughout the whole OCCT library.
The whole OCCT library is organized in a set of modules. The first module, providing most basic services and used by all other modules, is called Foundation Classes and described by this manual.
Every module consists primarily of one or several toolkits (though it can also contain executables, resource units etc.). Physically a toolkit is represented by a shared library (e.g. .so or .dll). The toolkit is built from one or several packages.
A package groups together a number of classes which have semantic links. For example, a geometry package would contain Point, Line, and Circle classes. A package can also contain enumerations, exceptions and package methods (functions). In practice, a class name is prefixed with the name of its package e.g. Geom_Circle. Data types described in a package may include one or more of the following data types:
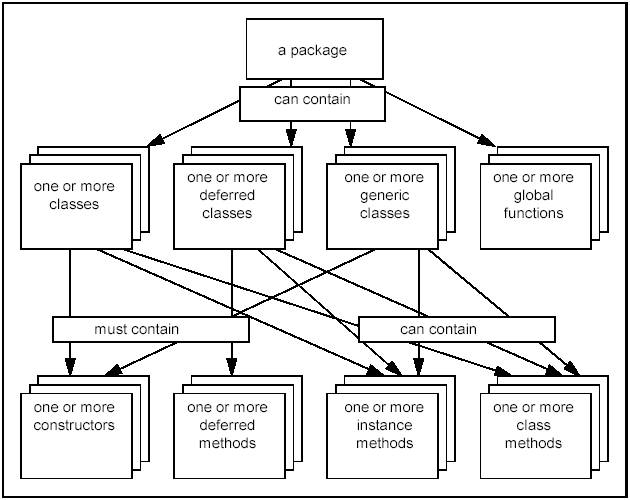
Methods are either functions or procedures. Functions return an object, whereas procedures only communicate by passing arguments. In both cases, when the transmitted object is an instance manipulated by a handle, its identifier is passed. There are three categories of methods:
The fundamental software component in object-oriented software development is the class. A class is the implementation of a data type. It defines its behavior (the services offered by its functions) and its representation (the data structure of the class – the fields, which store its data).
Classes fall into three categories:
The purpose of inheritance is to reduce the development workload. The inheritance mechanism allows a new class to be declared already containing the characteristics of an existing class. This new class can then be rapidly specialized for the task in hand. This avoids the necessity of developing each component "from scratch". For example, having already developed a class BankAccount you could quickly specialize new classes: SavingsAccount, LongTermDepositAccount, MoneyMarketAccount, RevolvingCreditAccount, etc....
The corollary of this is that when two or more classes inherit from a parent (or ancestor) class, all these classes guarantee as a minimum the behavior of their parent (or ancestor). For example, if the parent class BankAccount contains the method Print which tells it to print itself out, then all its descendant classes guarantee to offer the same service.
One way of ensuring the use of inheritance is to declare classes at the top of a hierarchy as being abstract. In such classes, the methods are not implemented. This forces the user to create a new class which redefines the methods. This is a way of guaranteeing a certain minimum of behavior among descendant classes.
An object-oriented language structures a system around data types rather than around the actions carried out on this data. In this context, an object is an instance of a data type and its definition determines how it can be used. Each data type is implemented by one or more classes, which make up the basic elements of the system.
The data types in Open CASCADE Technology fall into two categories:
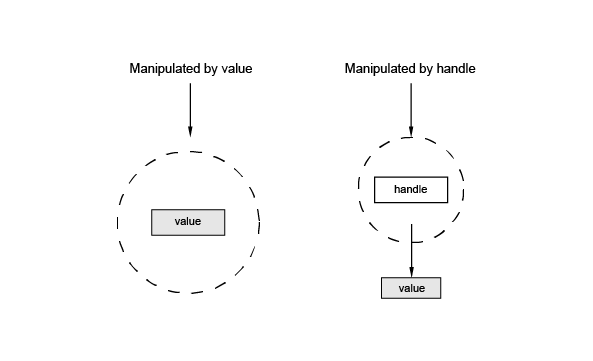
A data type is implemented as a class. The class not only defines its data representation and the methods available on instances, but it also suggests how the instance will be manipulated.
A variable of a type manipulated by handle which is not attached to an object is said to be null. To reference an object, we instantiate the class with one of its constructors. For example, in C++:
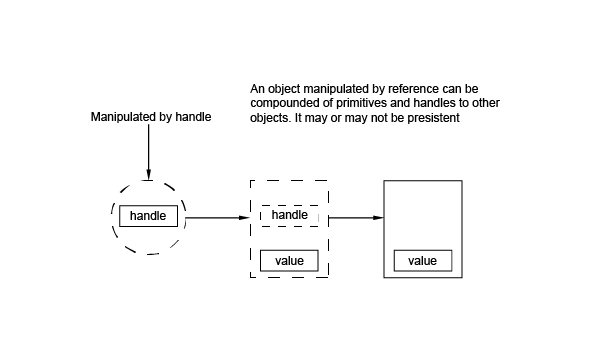
In Open CASCADE Technology, the Handles are specific classes that are used to safely manipulate objects allocated in the dynamic memory by reference, providing reference counting mechanism and automatic destruction of the object when it is not referenced.
The primitive types are predefined in the language and they are manipulated by value.
The services offered by each of these types are described in the Standard Package. The table below presents the equivalence existing between C++ fundamental types and OCCT primitive types.
Table 1: Equivalence between C++ Types and OCCT Primitive Types
| C++ Types | OCCT Types |
|---|---|
| int | Standard_Integer |
| double | Standard_Real |
| float | Standard_ShortReal |
| bool | Standard_Boolean |
| char | Standard_Character |
| char16_t | Standard_Utf16Char |
| char* | Standard_CString |
| void* | Standard_Address |
| char16_t* | Standard_ExtString |
Reminder of the classes listed above:
There are three categories of types which are manipulated by value:

These are types defined by classes inheriting from the Standard_Transient class.
When you design an object, it can be difficult to choose how to manipulate that object: by value or by handle. The following ideas can help you to make up your mind:
A handle is OCCT implementation of a smart pointer. Several handles can reference the same object. Also, a single handle may reference several objects, but only one at a time. To have access to the object it refers to, the handle must be de-referenced just as with a C++ pointer.
Class Standard_Transient is a root of a big hierarchy of OCCT classes that are said to be operable by handles. It provides a reference counter field, inherited by all its descendant classes, that is used by associated Handle() classes to track a number of handles pointing to this instance of the object.
Objects of classes derived (directly or indirectly) from Transient, are normally allocated in dynamic memory using operator new, and manipulated by handle. Handle is defined as template class opencascade::handle<>. Open CASCADE Technology provides preprocessor macro Handle() that is historically used throughout OCCT code to name a handle:
In addition, for most OCCT classes additional typedef is defined for a handle, as the name of a class prefixed by Handle_. For instance, the above example can be also coded as:
A handle is characterized by the object it references.
Before performing any operation on a transient object, you must declare the handle. For example, if Point and Line are two transient classes from the Geom package, you would write:
Declaring a handle creates a null handle that does not refer to any object. The handle may be checked to be null by its method IsNull(). To nullify a handle, use method Nullify().
To initialize a handle, either a new object should be created or the value of another handle can be assigned to it, on condition that their types are compatible.
Note that handles should only be used for object sharing. For all local operations, it is advisable to use classes manipulated by values.
Open CASCADE Technology provides a means to describe the hierarchy of data types in a generic way, with a possibility to check the exact type of the given object at run-time (similarly to C++ RTTI).
To enable this feature, a class declaration should include the declaration of OCCT RTTI. Header Standard_Type.hxx provides two variants of preprocessor macros facilitating this:
Out-of line variant, which uses one macro in the declaration (normally in the header file), and another in the implementation (in C++ source):
In Appli_ExtSurface.hxx file:
In Appli_ExtSurface.cxx file:
These macros define method DynamicType() that returns a type descriptor - handle to singleton instance of the class Standard_Type describing the class. The type descriptor stores the name of the class and the descriptor of its parent class.
Note that while inline version is easier to use, for widely used classes this method may lead to bloating of binary code of dependent libraries, due to multiple instantiations of inline method.
To get the type descriptor for a given class type, use macro STANDARD_TYPE() with the name of the class as argument.
Example of usage:
The type used in the declaration of a handle is the static type of the object, the type seen by the compiler. A handle can reference an object instantiated from a subclass of its static type. Thus, the dynamic type of an object (also called the actual type of an object) can be a descendant of the type which appears in the handle declaration through which it is manipulated.
Consider the class Geom_CartesianPoint, a sub-class of Geom_Point; the rule of type conformity can be illustrated as follows:
The compiler sees aPnt1 as a handle to Geom_Point though the actual object referenced by aPnt1 is of the Geom_CartesianPoint type.
According to the rule of type conformity, it is always possible to go up the class hierarchy through successive assignments of handles. On the other hand, assignment does not authorize you to go down the hierarchy. Consequently, an explicit type conversion of handles is required.
A handle can be converted explicitly into one of its sub-types if the actual type of the referenced object is a descendant of the object used to cast the handle. If this is not the case, the handle is nullified (explicit type conversion is sometimes called a "safe cast"). Consider the example below.
If conversion is not compatible with the actual type of the referenced object, the handle which was "cast" becomes null (and no exception is raised). So, if you require reliable services defined in a sub-class of the type seen by the handle (static type), write as follows:
Downcasting is used particularly with collections of objects of different types; however, these objects should inherit from the same root class.
For example, with a sequence of transient objects TColStd_SequenceOfTransient and two classes A and B that both inherit from Standard_Transient, you get the following syntax:
To create an object which is manipulated by handle, declare the handle and initialize it with the standard C++ new operator, immediately followed by a call to the constructor. The constructor can be any of those specified in the source of the class from which the object is instanced.
Unlike for a pointer, the delete operator does not work on a handle; the referenced object is automatically destroyed when no longer in use.
Once you have a handle to an object, you can use it like a pointer in C++. To invoke a method which acts on the referenced object, you translate this method by the standard arrow operator, or alternatively, by function call syntax when this is available.
To test or to modify the state of the handle, the method is translated by the dot operator. The example below illustrates how to access the coordinates of an (optionally initialized) point object:
The example below illustrates how to access the type object of a Cartesian point:
Standard_NullObject exception will be raised if a field or a method of an object is accessed via a Null handle.
A class method is called like a static C++ function, i.e. it is called by the name of the class of which it is a member, followed by the “::” operator and the name of the method.
For example, we can find the maximum degree of a Bezier curve:
Before you delete an object, you must ensure it is no longer referenced. To reduce the programming load related to this management of object life, the delete function in Open CASCADE Technology is secured by a reference counter of classes manipulated by handle. A handle automatically deletes an object when it is no longer referenced. Normally you never call the delete operator explicitly on instances of subclasses of Standard_Transient.
When a new handle to the same object is created, the reference counter is incremented. When the handle is destroyed, nullified, or reassigned to another object, that counter is decremented. The object is automatically deleted by the handle when reference counter becomes 0.
The principle of allocation can be seen in the example below.
You can easily cast a reference to the handle object to void* by defining the following:
Cycles appear if two or more objects reference each other by handles (stored as fields). In this condition automatic destruction will not work.
Consider for example a graph, whose objects (primitives) have to know the graph object to which they belong, i.e. a primitive must have a reference to complete graph object. If both primitives and the graph are manipulated by handle and they refer to each other by keeping a handle as a field, the cycle appears.
The graph object will not be deleted when the last handle to it is destructed in the application, since there are handles to it stored inside its own data structure (primitives).
There are two approaches how to avoid such situation:
In a work session, geometric modeling applications create and delete a considerable number of C++ objects allocated in the dynamic memory (heap). In this context, performance of standard functions for allocating and deallocating memory may be not sufficient. For this reason, Open CASCADE Technology employs a specialized memory manager implemented in the Standard package.
The Memory Manager is based on the following principles:
As a general rule, it is advisable to allocate memory through significant blocks. In this way, the user can work with blocks of contiguous data and it facilitates memory page manager processing.
To allocate memory in a C code with Open CASCADE Technology memory manager, simply use method Standard::Allocate() instead of malloc() and method Standard::Free() instead of free(). In addition, method Standard::Reallocate() is provided to replace C function realloc().
In C++, operators new() and delete() for a class may be defined so as to allocate memory using Standard::Allocate() and free it using Standard::Free(). In that case all objects of that class and all inherited classes will be allocated using the OCCT memory manager.
Preprocessor macro DEFINE_STANDARD_ALLOC provided by header Standard_DefineAlloc.hxx defines new() and delete() in this way. It is used for all OCCT classes (apart from a few exceptions) which thus are allocated using the OCCT memory manager. Since operators new() and delete() are inherited, this is also true for any class derived from an OCCT class, for instance, for all classes derived from Standard_Transient.
Note that it is possible (though not recommended unless really unavoidable) to redefine new() and delete() functions for a class inheriting Standard_Transient. If that is done, the method Delete() should be also redefined to apply operator delete to this pointer. This will ensure that appropriate delete() function will be called, even if the object is manipulated by a handle to a base class.
The OCCT memory manager may be configured to apply different optimization techniques to different memory blocks (depending on their size), or even to avoid any optimization and use C functions malloc() and free() directly. The configuration is defined by numeric values of the following environment variables:
When MMGT_OPT is set to 1, the following optimization techniques are used:
In the current version memory pools are never returned to the system (until the process finishes). However, memory blocks that are released by the method Standard::Free() are remembered in the free lists and later reused when the next block of the same size is allocated (recycling).
However, unlike small blocks, the recycled medium blocks contained in the free lists (i.e. released by the program but held by the memory manager) can be returned to the heap by method Standard::Purge().
The major benefit of the OCCT memory manager is explained by its recycling of small and medium blocks that makes an application work much faster when it constantly allocates and frees multiple memory blocks of similar sizes. In practical situations, the real gain on the application performance may be up to 50%.
The associated drawback is that recycled memory is not returned to the operating system during program execution. This may lead to considerable memory consumption and even be misinterpreted as a memory leak. To minimize this effect it is necessary to call the method Standard::Purge after the completion of memory-intensive operations.
The overhead expenses induced by the OCCT memory manager are:
Note that these overheads may be greater or less than overheads induced by the C heap memory manager, so overall memory consumption may be greater in either optimized or standard modes, depending on circumstances.
As a general rule, it is advisable to allocate memory through significant blocks. In this way, you can work with blocks of contiguous data, and processing is facilitated for the memory page manager.
OCCT memory manager uses mutex to lock access to free lists, therefore it may have less performance than non-optimized mode in situations when different threads often make simultaneous calls to the memory manager. The reason is that modern implementations of malloc() and free() employ several allocation arenas and thus avoid delays waiting mutex release, which are possible in such situations.
The behavior of any object is implemented by the methods, which were defined in its class declaration. The definition of these methods includes not only their signature (their programming interface) but also their domain of validity.
This domain is expressed by exceptions. Exceptions are raised under various error conditions to protect software quality.
Exception handling provides a means of transferring control from a given point in a program being executed to an exception handler associated with another point previously executed.
A method may raise an exception which interrupts its normal execution and transfers control to the handler catching this exception.
A hierarchy of commonly used exception classes is provided. The root class is Standard_Failure from the Standard package. So each exception inherits from Standard_Failure either directly or by inheriting from another exception. Exception classes list all exceptions, which can be raised by any OCCT function.
Open CASCADE Technology also provides support for converting system signals (such as access violation or division by zero) to exceptions, so that such situations can be safely handled with the same uniform approach.
However, in order to support this functionality on various platforms, some special methods and workarounds are used. Though the implementation details are hidden and handling of OCCT exceptions is done basically in the same way as with C++, some peculiarities of this approach shall be taken into account and some rules must be respected.
The following paragraphs describe recommended approaches for using exceptions when working with Open CASCADE Technology.
The following example:
raises an exception of Standard_DomainError type with the associated message "Cannot cope with this condition", the message being optional. This exception may be caught by a handler of a Standard_DomainError type as follows:
Exceptions should not be used as a programming technique, to replace a "goto" statement for example, but as a way to protect methods against misuse. The caller must make sure its condition is such that the method can cope with it.
Thus,
For example, if you consider the TCollection_Array1 class used with:
then, the Value function may be implemented as follows:
Here validity of the index is first verified using the Lower and Upper functions in order to protect the call. Normally the caller ensures the index being in the valid range before calling Value(). In this case the above implementation of Value is not optimal since the test done in Value is time-consuming and redundant.
It is a widely used practice to include that kind of protections in a debug build of the program and exclude in release (optimized) build. To support this practice, the macros Raise_if() are provided for every OCCT exception class:
where ErrorTypeName is the exception type, condition is the logical expression leading to the raise of the exception, and Error message is the associated message.
The entire call may be removed by defining one of the preprocessor symbols No_Exception or No_<ErrorTypeName> at compile-time:
Using this syntax, the Value function becomes:
When an exception is raised, control is transferred to the nearest handler of a given type in the call stack, that is:
A handler of T exception type is a match for a raise expression with an exception type of E if:
In order to handle system signals as exceptions, make sure to insert macro OCC_CATCH_SIGNALS somewhere in the beginning of the relevant code. The recommended location for it is first statement after opening brace of try {} block.
As an example, consider the exceptions of type Standard_NumericError, Standard_Overflow, Standard_Underflow and Standard_DivideByZero, where Standard_NumericError is the parent type of the three others.
Here, the first handler will catch exceptions of Standard_Overflow type and the second one – exceptions of Standard_NumericError type and all exceptions derived from it, including Standard_Underflow and Standard_DivideByZero.
The handlers are checked in order of appearance, from the nearest to the try block to the most distant from it, until one matches the raise expression. For a try block, it would be a mistake to place a handler for a base exception type ahead of a handler for its derived type since that would ensure that the handler for the derived exception would never be invoked.
The exceptions form a hierarchy tree completely separated from other user defined classes. One exception of type Standard_Failure is the root of the entire exception hierarchy. Thus, using a handler with Standard_Failure type catches any OCCT exception. It is recommended to set up such a handler in the main routine.
The main routine of a program would look like this:
Though standard C++ scoping rules and syntax apply to try block and handlers, note that on some platforms Open CASCADE Technology may be compiled in compatibility mode when exceptions are emulated by long jumps (see below). In this mode it is required that no statement precedes or follows any handler. Thus it is highly recommended to always include a try block into additional {} braces. Also this mode requires that header file Standard_ErrorHandler.hxx be included in your program before a try block, otherwise it may fail to handle Open CASCADE Technology exceptions.
In order for the application to be able to catch system signals (access violation, division by zero, etc.) in the same way as other exceptions, the appropriate signal handler shall be installed in the runtime by the method OSD::SetSignal().
Normally this method is called in the beginning of the main() function. It installs a handler that will convert system signals into OCCT exceptions.
In order to actually convert signals to exceptions, macro OCC_CATCH_SIGNALS needs to be inserted in the source code. The typical place where this macro is put is beginning of the try{} block which catches such exceptions.
The exception handling mechanism in Open CASCADE Technology is implemented in different ways depending on the preprocessor macro OCC_CONVERT_SIGNALS, which shall be consistently defined by compilation procedures for both Open CASCADE Technology and user applications:
On Linux, macro OCC_CONVERT_SIGNALS is defined by default. The C++ exception mechanism is used for catching exceptions and for throwing them from normal code. Since it is not possible to throw C++ exception from system signal handler function, that function makes a long jump to the nearest (in the execution stack) invocation of macro OCC_CATCH_SIGNALS, and only there the C++ exception gets actually thrown. The macro OCC_CATCH_SIGNALS is defined in the file Standard_ErrorHandler.hxx. Therefore, including this file is necessary for successful compilation of a code containing this macro.
This mode differs from standard C++ exception handling only for signals:
In general, for writing platform-independent code it is recommended to insert macros OCC_CATCH_SIGNALS in try {} blocks or other code where signals may happen.
A plug-in is a component that can be loaded dynamically into a client application, not requiring to be directly linked to it. The plug-in is not bound to its client, i.e. the plug-in knows only how its connection mechanism is defined and how to call the corresponding services.
A plug-in can be used to:
The plug-in is identified with the help of the global universal identifier (GUID). The GUID includes lower case characters and cannot end with a blank space.
Once it has been loaded, the call to the services provided by the plug-in is direct (the client is implemented in the same language as the plug-in).
The C++ plug-in implements a service as an object with functions defined in an abstract class (this abstract class and its parent classes with the GUID are the only information about the plug-in implemented in the client application). The plug-in consists of a shareable library including a method named Factory which creates the C++ object (the client cannot instantiate this object because the plug-in implementation is not visible). Foundation classes provide in the package Plugin a method named Load(), which enables the client to access the required service through a library.
That method reads the information regarding available plug-ins and their locations from the resource file Plugin found by environment variable CSF_PluginDefaults:
The Load method looks for the library name in the resource file or registry through its GUID, for example, on UNIX:
Then the Load method loads the library according to the rules of the operating system of the host machine (for example, by using environment variables such as LD_LIBRARY_PATH with Unix and PATH with Windows). After that it invokes the PLUGINFACTORY method to return the object, which supports the required service. The client may then call the functions supported by this object.
To invoke one of the services provided by the plug-in, you may call the Plugin::Load() global function with the Standard_GUID of the requested service as follows:
Let us take FAFactory.hxx and FAFactory.cxx as an example:
Application might also instantiate a factory by linking to the library and calling FAFactory::Factory() directly.
The Collections component contains the classes that handle dynamically sized aggregates of data. They include a wide range of collections such as arrays, lists and maps.
Some OCCT collections have close friends in modern STL (standard templates collection), but define a little bit different properties or behavior. OCCT gives user a wider choice, but it is up to user to decide which particular OCCT or STL collection is most suitable for specific algorithm (including performance and usage convenience). OCCT itself highly relies on its own collections for historical reasons - many features implemented by OCCT were unavailable in earlier versions of STL.
Collections classes are generic (C++ templates), that is, they define a structure and algorithms allowing to hold a variety of objects which do not necessarily inherit from a unique root class.
Note that:
The Collections component provides a wide range of generic collections:
Macro definitions of these classes are stored in NCollection_Define*.hxx files. These definitions are now obsolete though still can be used, particularly for compatibility with the existing code.
Let see an example of NCollection template class instantiation for a sequence of points in the header file MyPackage_SequenceOfPnt.hxx (analogue of TColgp_SequenceOfPnt):
For the case, when sequence itself should be managed by handle, auxiliary macros DEFINE_HSEQUENCE can be used:
See more details about available collections in following sections.
Standard collections provided by OCCT are:
These classes provide STL-style iterators (methods begin() and end()) and thus can be used in STL algorithms.
These are unidimensional arrays similar to C arrays, i.e. of fixed size but dynamically dimensioned at construction time. As with a C array, the access time for an NCollection_Array1 indexed item is constant and is independent of the array size. Arrays are commonly used as elementary data structures for more complex objects.
This template class depends on Item, the type of element in the array. Array indexation starts and ends at a position given to class constructor. Thus, when accessing an item, you must base the index on the lower and upper bounds of the array.
These are bi-dimensional arrays of fixed size but dynamically dimensioned at construction time.
As with a C array, the access time for an NCollection_Array2 indexed item is constant and is independent of the array size. Arrays are commonly used as elementary data structures for more complex objects.
This template class depends on Item, the type of element in the array. Array indexation starts and ends at a position given to class constructor. Thus, when accessing an item, you must base the index on the lower and upper bounds of the array.
These are ordered lists of non-unique objects which can be accessed sequentially using an NCollection_List::Iterator. Item insertion in a list is very fast at any position. But searching for items by value may be slow if the list is long, because it requires a sequential search.
This template class depends on Item, the type of element in the structure. A sequence is a better structure when searching for items by value. Queues and stacks are other kinds of list with a different access to data.
This is a sequence of items indexed by an integer. Sequences have about the same goal as unidimensional arrays (NCollection_Array1): they are commonly used as elementary data structures for more complex objects. But a sequence is a structure of variable size: sequences avoid the use of large and quasi-empty arrays. Exploring a sequence data structure is effective when the exploration is done in sequence; elsewhere a sequence item is longer to read than an array item. Note also that sequences are not effective when they have to support numerous algorithmic explorations: a map is better for that.
This template class depends on Item, the type of element in the sequence. The first element in sequence has index equal to 1.
Class NCollection_Vector is implemented internally as a list of arrays of the same size. Its properties:
Insertion in a Vector-type class is made by two methods:
Other essential properties coming from NCollection_List and NCollection_Array1 type collections:
The first element in vector has index equal to 0.
Class NCollection_SparseArray has almost the same features as NCollection_Vector, but it allows to store items having scattered indices. In NCollection_Vector, if you set an item with index 1000000, the container will allocate memory for all items with indices in the range 0-1000000. In NCollection_SparseArray, only one small block of items will be reserved that contains the item with index 1000000.
This class can be also seen as equivalence of NCollection_DataMap<int,TheItemType> with the only one practical difference: it can be much less memory-expensive if items are small (e.g. Integer or Handle).
This type has both interfaces of NCollection_DataMap and NCollection_Vector to access items.
OCCT provides several classes for storage of objects by value, providing fast search due to use of hash:
Maps are dynamically extended data structures where data is quickly accessed with a key. Once inserted in the map, a map item is referenced as an entry of the map. Maps avoid the use of large and quasi-empty arrays.
Each entry of the map is addressed by a key. Two different keys address two different entries of the map. The position of an entry in the map is called a bucket.
A map is dimensioned by its number of buckets, i.e. the maximum number of entries in the map. The hashing function transforms a key into a bucket index. The number of values that can be computed by the hashing function is equal to the number of buckets of the map.
Both the hashing function and the equality test between two keys are provided by a hasher object.
The access time for a map item is much better than the one for a sequence, list, queue or stack item. It is comparable with the access time for an array item. It depends on the size of the map (number of buckets) and on the quality of the user redefinable hashing function.
Keys, items and hashers are parameters of these OCCT map templates. NCollection_DefaultHasher class describes the functions required by any hasher, which is to be used with a map instantiated from the NCollection component.
A map may be explored by a map iterator. This exploration provides only inserted entries in the map (i.e. non empty buckets).
This is a map used to store keys with associated items. An entry of NCollection_DataMap is composed of both the key and the item. The NCollection_DataMap can be seen as an extended array where the keys are the indexes.
NCollection_DataMap is a template class which depends on three parameters:
Use a NCollection_DataMap::Iterator to explore a NCollection_DataMap map. NCollection_DefaultHasher class describes the functions required for a Hasher object.
This is a map used to bind pairs of keys (Key1,Key2) and retrieve them in linear time.
Key1 is referenced as the first key of the NCollection_DoubleMap and Key2 as the second key.
An entry of a NCollection_DoubleMap is composed of a pair of two keys: the first key and the second key.
NCollection_DoubleMap is a template class which depends on four parameters:
Use NCollection_DoubleMap::Iterator to explore a NCollection_DoubleMap map. NCollection_DefaultHasher class describes the functions required for a Hasher1 or a Hasher2 object.
This is map to store keys with associated items and to bind an index to them.
Each new key stored in the map is assigned an index. Indexes are incremented as keys (and items) stored in the map. A key can be found by the index, and an index can be found by the key. No key but the last can be removed, so the indexes are in the range 1...Upper, where Upper is the number of keys stored in the map. An item is stored with each key.
An entry of an NCollection_IndexedDataMap is composed of both the key, the item and the index. An NCollection_IndexedDataMap is an ordered map, which allows a linear iteration on its contents. It combines the interest:
NCollection_IndexedDataMap is a template class which depends on three parameters:
This is map used to store keys and to bind an index to them.
Each new key stored in the map is assigned an index. Indexes are incremented as keys stored in the map. A key can be found by the index, and an index by the key. No key but the last can be removed, so the indexes are in the range 1...Upper where Upper is the number of keys stored in the map.
An entry of an NCollection_IndexedMap is composed of both the key and the index. An NCollection_IndexedMap is an ordered map, which allows a linear iteration on its contents. But no data is attached to the key. An NCollection_IndexedMap is typically used by an algorithm to know if some action is still performed on components of a complex data structure.
NCollection_IndexedMap is a template class which depends on two parameters:
This is a basic hashed map, used to store and retrieve keys in linear time.
An entry of a NCollection_Map is composed of the key only. No data is attached to the key. An NCollection_Map is typically used by an algorithm to know if some action is still performed on components of a complex data structure.
NCollection_Map is a generic class which depends on two parameters:
Use a NCollection_Map::Iterator to explore a NCollection_Map map.
This is a default hasher on the keys of a map instantiated from the NCollection component.
A hasher provides two functions:
Hashers are used as parameters in template maps provided by the NCollection component.
NCollection_DefaultHasher is a template class which depends on the type of keys, providing that Key is a type from the Standard package. In such cases NCollection_DefaultHasher may be directly instantiated with Key. Note that the package TColStd provides some of these instantiations.
Elsewhere, if Key is not a type from the Standard package you must consider NCollection_DefaultHasher as a template and build a class which includes its functions, in order to use it as a hasher in a map instantiated from the NCollection component.
Note that TCollection_AsciiString and TCollection_ExtendedString classes correspond to these specifications, in consequence they may be used as hashers: when Key is one of these two types you may just define the hasher as the same type at the time of instantiation of your map.
Every collection defines its Iterator class capable of iterating the members in some predefined order. Every Iterator is defined as a subtype of the particular collection type (e.g., MyPackage_StackOfPnt::Iterator). The order of iteration is defined by a particular collection type.
The common methods of Iterator are:
| Name | Method | Description |
|---|---|---|
| Init() | void Init (MyCollection& ) | Initializes the iterator on the collection object |
| More() | bool More() | Makes a query if there is another non-iterated member |
| Next() | void Next() | Increments the iterator |
| Value() | const ItemType& Value() | Returns the current member |
| ChangeValue() | ItemType& ChangeValue() | Returns the mutable current member |
Usage sample:
All constructors of NCollection classes receive the Allocator object as the last parameter. This is an object of a type managed by Handle, inheriting NCollection_BaseAllocator, with the following (mandatory) methods redefined:
It is used internally every time when the collection allocates memory for its item(s) and releases this memory. The default value of this parameter (empty Handle) designates the use of NCollection_BaseAllocator, where the functions Standard::Allocate and Standard::Free are called. Therefore if the user of NCollection does not specify any allocator as a parameter to the constructor of his collection, the memory management will be identical to other Open CASCADE Technology classes.
Nevertheless, it is possible to define a custom Allocator type to manage the memory in the most optimal or convenient way for this algorithm.
As one possible choice, the class NCollection_IncAllocator is included. Unlike NCollection_BaseAllocator, the memory is allocated in big blocks (about 12kB) and the allocator keeps track of the amount of occupied memory. The method Allocate just increments the pointer to non-occupied memory and returns its previous value. Memory is only released in the destructor of NCollection_IncAllocator, the method Free is empty. If used properly, this Allocator can greatly improve the performance of specific algorithms.
OCCT provides several data structures for optimized traverse of large collection of objects based on their locality (in 3D space).
The class name NCollection_UBTree stands for "Unbalanced Binary Tree". It stores the members in a binary tree of overlapped bounding objects (boxes or else). Once the tree of boxes of geometric objects is constructed, the algorithm is capable of fast geometric selection of objects. The tree can be easily updated by adding to it a new object with bounding box. The time of adding to the tree of one object is O(log(N)), where N is the total number of objects, so the time of building a tree of N objects is O(N(log(N)). The search time of one object is O(log(N)).
Defining various classes inheriting NCollection_UBTree::Selector we can perform various kinds of selection over the same b-tree object.
The object may be of any type allowing copying. Among the best suitable solutions there can be a pointer to an object, handled object or integer index of object inside some collection.
The bounding object may have any dimension and geometry. The minimal interface of TheBndType (besides public empty and copy constructor and operator=) used in NCollection_UBTree algorithm as follows:
This interface is implemented in types of Bnd package: Bnd_Box, Bnd_Box2d, Bnd_B2x, Bnd_B3x.
To select objects you need to define a class derived from NCollection_UBTree::Selector that should redefine the necessary virtual methods to maintain the selection condition. Usually this class instance is also used to retrieve selected objects after search. The class NCollection_UBTreeFiller is used to randomly populate a NCollection_UBTree instance. The quality of a tree is better (considering the speed of searches) if objects are added to it in a random order trying to avoid the addition of a chain of nearby objects one following another. Instantiation of NCollection_UBTreeFiller collects objects to be added, and then adds them at once to the given NCollection_UBTree instance in a random order using the Fisher-Yates algorithm. Below is the sample code that creates an instance of NCollection_UBTree indexed by 2D boxes (Bnd_B2f), then a selection is performed returning the objects whose bounding boxes contain the given 2D point.
Class NCollection_CellFilter represents a data structure for sorting geometric objects in n-dimensional space into cells, with associated algorithm for fast checking of coincidence (overlapping, intersection, etc.) with other objects. It can be considered as a functional alternative to NCollection_UBTree, as in the best case it provides the direct access to an object like in an n-dimensional array, while search with NCollection_UBTree provides logarithmic law access time.
Packages TShort, TColGeom, TColGeom2d, TColStd, TColgp provide template instantiations (typedefs) of NCollection templates to standard OCCT types. Classes with H prefix in name are handle-based variants and inherit Standard_Transient.
Packages like TopTools also include definitions of collections and hash functions for complex types like shapes – TopTools_ShapeMapHasher, TopTools_MapOfShape.
Apart from that class TColStd_PackedMapOfInteger provides an alternative implementation of map of integer numbers, optimized for both performance and memory usage (it uses bit flags to encode integers, which results in spending only 24 bytes per 32 integers stored in optimal case). This class also provides Boolean operations with maps as sets of integers (union, intersection, subtraction, difference, checks for equality and containment).
TCollection_AsciiString defines a variable-length sequence of UTF-8 code points (normal 8-bit character type), while TCollection_ExtendedString stores UTF-16/UCS-2 code points (16-bit character type). Both follow value semantics - that is, they are the actual strings, not handles to strings, and are copied through assignment. TCollection_HAsciiString / TCollection_HExtendedString are handle wrappers over TCollection_AsciiString / TCollection_ExtendedString.
String classes provide the following services to manipulate character strings:
TCollection_AsciiString and TCollection_ExtendedString provide UTF-8 <-> UTF-16 conversion constructors, making these string classes interchangeable. Resource_Unicode provides functions to convert strings given in ANSI, EUC, GB or SJIS format, to a Unicode string and vice versa. NCollection_UtfIterator class implements an iterator over multibyte UTF-8/UTF-16 strings as a sequence of UTF-32 Unicode symbols.
Quantities are various classes supporting date and time information and color.
Quantity classes provide the following services:
A mathematical quantity is characterized by the name and the value (real).
A physical quantity is characterized by the name, the value (real) and the unit. The unit may be either an international unit complying with the International Unit System (SI) or a user defined unit. The unit is managed by the physical quantity user.
The UnitsAPI global functions are used to convert a value from any unit into another unit. Conversion is executed among three unit systems:
The SI System is the standard international unit system. It is indicated by SI in the signatures of the UnitsAPI functions.
The OCCT (former MDTV) System corresponds to the SI international standard but the length unit and all its derivatives use the millimeter instead of the meter.
Both systems are proposed by Open CASCADE Technology; the SI System is the standard option. By selecting one of these two systems, you define your Local System through the SetLocalSystem function. The Local System is indicated by LS in the signatures of the UnitsAPI functions. The Local System units can be modified in the working environment. You define your Current System by modifying its units through the SetCurrentUnit function. The Current System is indicated by Current in the signatures of the UnitsAPI functions. A physical quantity is defined by a string (example: LENGTH).
Math primitives and algorithms available in Open CASCADE Technology include:
The Vectors and Matrices component provides a C++ implementation of the fundamental types math_Vector and math_Matrix, which are regularly used to define more complex data structures.
The math_Vector and math_Matrix classes provide commonly used mathematical algorithms which include:
These classes also provide a data structure to represent any expression, relation, or function used in mathematics, including the assignment of variables.
Vectors and matrices have arbitrary ranges which must be defined at declaration time and cannot be changed after declaration.
Vector and Matrix objects use value semantics. In other words, they cannot be shared and are copied through assignment.
Vector and Matrix values may be initialized and obtained using indexes which must lie within the range definition of the vector or the matrix.
Some operations on Vector and Matrix objects may not be legal. In this case an exception is raised. Two standard exceptions are used:
Open CASCADE Technology primitive geometric types are a STEP-compliant implementation of basic geometric and algebraic entities. They provide:
All these functions are provided by geometric processor package gp. Its classes for 2d and 3d objects are handled by value rather than by reference. When this sort of object is copied, it is copied entirely. Changes in one instance will not be reflected in another.
The gp package defines the basic geometric entities used for algebraic calculation and basic analytical geometry in 2d & 3d space. It also provides basic transformations such as identity, rotation, translation, mirroring, scale transformations, combinations of transformations, etc. Entities are handled by value.
Note that gp curves and surfaces are analytic: there is no parameterization and no orientation on gp entities, i.e. these entities do not provide functions which work with these properties.
If you need, you may use more evolved data structures provided by Geom (in 3D space) and Geom2d (in the plane). However, the definition of gp entities is identical to the one of equivalent Geom and Geom2d entities, and they are located in the plane or in space with the same kind of positioning systems. They implicitly contain the orientation, which they express on the Geom and Geom2d entities, and they induce the definition of their parameterization.
Therefore, it is easy to give an implicit parameterization to gp curves and surfaces, which is the parametrization of the equivalent Geom or Geom2d entity. This property is particularly useful when computing projections or intersections, or for operations involving complex algorithms where it is particularly important to manipulate the simplest data structures, i.e. those of gp. Thus, ElCLib and ElSLib packages provide functions to compute:
Note: the gp entities cannot be shared when they are inside more complex data structures.
Before creating a geometric object, you must decide whether you are in a 2d or in a 3d context and how you want to handle the object. If you do not need a single instance of a geometric primitive but a set of them then the package which deals with collections of this sort of object, TColgp, will provide the necessary functionality. In particular, this package provides standard and frequently used instantiations of generic classes with geometric objects, i.e. gp_XY, gp_XYZ, gp_Pnt, gp_Pnt2d, gp_Vec, gp_Vec2d, gp_Lin, gp_Lin2d, gp_Circ, gp_Circ2d.
There are various library packages available which offer a range of basic computations on curves and surfaces. If you are dealing with objects created from the gp package, the useful algorithms are in the elementary curves and surfaces libraries – the ElCLib and ElSLib packages.
Additionally, Bnd package provides a set of classes and tools to operate with bounding boxes of geometric objects in 2d and 3d space.
The common math algorithms library provides a C++ implementation of the most frequently used mathematical algorithms. These include:
All mathematical algorithms are implemented using the same principles. They contain:
The example below demonstrates the use of the math_Gauss class, which implements the Gauss solution for a set of linear equations. The following definition is an extract from the header file of the class math_Gauss:
Now the main program uses the math_Gauss class to solve the equations a*x1=b1 and a*x2=b2:
The next example demonstrates the use of the math_BissecNewton class, which implements a combination of the Newton and Bissection algorithms to find the root of a function known to lie between two bounds. The definition is an extract from the header file of the class math_BissecNewton:
The abstract class math_FunctionWithDerivative describes the services which have to be implemented for the function f which is to be used by a math_BissecNewton algorithm. The following definition corresponds to the header file of the abstract class math_FunctionWithDerivative:
Now the test sample uses the math_BissecNewton class to find the root of the equation f(x)=x**2-4 in the interval [1.5, 2.5]. The function to solve is implemented in the class myFunction which inherits from the class math_FunctionWithDerivative, then the main program finds the required root.
On the OCCT platform, each object stored in the database should carry its own precision value. This is important when dealing with systems where objects are imported from other systems as well as with various associated precision values.
The Precision package addresses the daily problem of the geometric algorithm developer: what precision setting to use to compare two numbers. Real number equivalence is clearly a poor choice. The difference between the numbers should be compared to a given precision setting.
Do not write if (X1 == X2), instead write if (Abs(X1-X2) < Precision).
Also, to order real numbers, keep in mind that if (X1 < X2 - Precision) is incorrect. if (X2 - X1 > Precision) is far better when X1 and X2 are high numbers.
This package proposes a set of methods providing precision settings for the most commonly encountered situations.
In Open CASCADE Technology, precision is usually not implicit; low-level geometric algorithms accept precision settings as arguments. Usually these should not refer directly to this package.
High-level modeling algorithms have to provide a precision setting to the low level geometric algorithms they call. One way is to use the settings provided by this package. The high-level modeling algorithms can also have their own strategy for managing precision. As an example the Topology Data Structure stores precision values which are later used by algorithms. When a new topology is created, it takes the stored value.
Different precision settings offered by this package cover the most common needs of geometric algorithms such as Intersection and Approximation. The choice of a precision value depends both on the algorithm and on the geometric space. The geometric space may be either:
The choice of precision value for parametric space depends not only on the accuracy of the machine, but also on the dimensions of the curve or the surface. This is because it is desirable to link parametric precision and real precision. If you are on a curve defined by the equation P(t), you would want to have equivalence between the following:
The Precision package offers a number of package methods and default precisions for use in dealing with angles, distances, intersections, approximations, and parametric space. It provides values to use in comparisons to test for real number equalities.
This package provides a set of real space precision values for algorithms. The real space precisions are designed for precision to 0.1 nanometers (in case if model is defined in millimeters).
The parametric precisions are derived from the real precisions by the Parametric function. This applies a scaling factor which is the length of a tangent to the curve or the surface. You, the user, provide this length. There is a default value for a curve with [0,1] parameter space and a length less than 100 meters.
The geometric packages provide Parametric precisions for the different types of curves. The Precision package provides methods to test whether a real number can be considered to be infinite.
This method is used to compare two angles. Its current value is Epsilon(2 * PI) i.e. the smallest number x such that 2*PI + x is different of 2*PI.
It can be used to check confusion of two angles as follows:
It is also possible to check parallelism of two vectors as follows:
Note that Precision::Angular() can be used on both dot and cross products because for small angles the Sine and the Angle are equivalent. So to test if two directions of type gp_Dir are perpendicular, it is legal to use the following code:
This method is used to test 3D distances. The current value is 1.e-7, in other words, 1/10 micron if the unit used is the millimeter.
It can be used to check confusion of two points as follows: ~~~~{.cpp} bool areEqualPoints (const gp_Pnt& thePnt1, const gp_Pnt& thePnt2) { return thePnt1.IsEqual (thePnt2, Precision::Confusion()); } ~~~
It is also possible to find a vector of null length:
This is reasonable precision to pass to an Intersection process as a limit of refinement of Intersection Points. Intersection is high enough for the process to converge quickly. Intersection is lower than Confusion so that you still get a point on the intersected geometries. The current value is Confusion() / 100.
This is a reasonable precision to pass to an approximation process as a limit of refinement of fitting. The approximation is greater than the other precisions because it is designed to be used when the time is at a premium. It has been provided as a reasonable compromise by the designers of the Approximation algorithm. The current value is Confusion() * 10. Note that Approximation is greater than Confusion, so care must be taken when using Confusion in an approximation process.