|
| virtual Standard_Integer | NbVariables () const |
| | returns the number of variables of the energy. More...
|
| |
| virtual Standard_Boolean | Value (const math_Vector &X, Standard_Real &E) |
| | computes the values of the Energys E for the variable <X>. Returns True if the computation was done successfully, False otherwise. More...
|
| |
| virtual Standard_Boolean | Gradient (const math_Vector &X, math_Vector &G) |
| | computes the gradient <G> of the energys for the variable <X>. Returns True if the computation was done successfully, False otherwise. More...
|
| |
| virtual Standard_Boolean | Values (const math_Vector &X, Standard_Real &E, math_Vector &G) |
| | computes the Energy <E> and the gradient <G> of the energy for the variable <X>. Returns True if the computation was done successfully, False otherwise. More...
|
| |
| virtual Standard_Boolean | Values (const math_Vector &X, Standard_Real &E, math_Vector &G, math_Matrix &H) |
| | computes the Energy <E>, the gradient <G> and the Hessian <H> of the energy for the variable <X>. Returns True if the computation was done successfully, False otherwise. More...
|
| |
| virtual Standard_Boolean | Variable (math_Vector &X) const |
| | compute the variables <X> wich correspond with the field <MyPoles> More...
|
| |
| const Handle< TColgp_HArray1OfPnt2d > & | Poles () const |
| | return the poles More...
|
| |
| virtual Standard_Integer | GetStateNumber () |
| | return the state of the function corresponding to the latestt call of any methods associated to the function. This function is called by each of the algorithms described later which define the function Integer Algorithm::StateNumber(). The algorithm has the responsibility to call this function when it has found a solution (i.e. a root or a minimum) and has to maintain the association between the solution found and this StateNumber. Byu default, this method returns 0 (which means for the algorithm: no state has been saved). It is the responsibility of the programmer to decide if he needs to save the current state of the function and to return an Integer that allows retrieval of the state. More...
|
| |
| virtual | ~math_MultipleVarFunction () |
| |
|
| | FairCurve_Energy (const Handle< TColgp_HArray1OfPnt2d > &Poles, const Standard_Integer ConstrOrder1, const Standard_Integer ConstrOrder2, const Standard_Boolean WithAuxValue=Standard_False, const Standard_Real Angle1=0, const Standard_Real Angle2=0, const Standard_Integer Degree=2, const Standard_Real Curvature1=0, const Standard_Real Curvature2=0) |
| | Angles corresspond to the Ox axis ConstrOrder1(2) can be equal to 0, 1 or 2. More...
|
| |
| void | Gradient1 (const math_Vector &TheVector, math_Vector &G) |
| | It is use internaly to make the Gradient Vector <G> More...
|
| |
| void | Hessian1 (const math_Vector &TheVector, math_Matrix &H) |
| | It is use internaly to make the Hessian Matrix <H> More...
|
| |
| virtual void | ComputePoles (const math_Vector &X) |
| | compute the poles wich correspond with the variable X More...
|
| |
| Standard_Integer | Indice (const Standard_Integer i, const Standard_Integer j) const |
| |
| void | ComputePolesG1 (const Standard_Integer Side, const Standard_Real Lambda, const gp_Pnt2d &P1, gp_Pnt2d &P2) const |
| | compute the pole wich depend of variables and G1 constraint More...
|
| |
| void | ComputePolesG2 (const Standard_Integer Side, const Standard_Real Lambda, const Standard_Real Rho, const gp_Pnt2d &P1, gp_Pnt2d &P2) const |
| | compute the pole wich depend of variables and G2 constraint More...
|
| |
| virtual Standard_Boolean | Compute (const Standard_Integer DerivativeOrder, math_Vector &Result)=0 |
| | compute the energy (and derivatives) in intermediat format More...
|
| |
necessary methodes to compute the energy of an FairCurve.
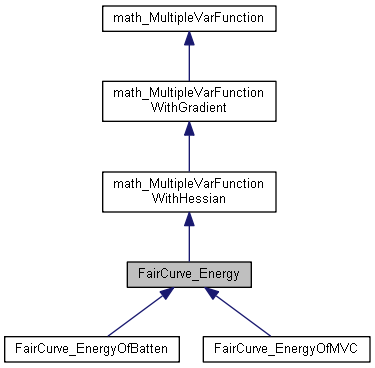
 Public Member Functions inherited from math_MultipleVarFunction
Public Member Functions inherited from math_MultipleVarFunction 1.8.10
1.8.10