Modeling Data supplies data structures to represent 2D and 3D geometric models.
This manual explains how to use Modeling Data.
Geometry Utilities provide the following services:
In modeling, it is often required to approximate or interpolate points into curves and surfaces. In interpolation, the process is complete when the curve or surface passes through all the points; in approximation, when it is as close to these points as possible.
Approximation of Curves and Surfaces groups together a variety of functions used in 2D and 3D geometry for:
You can program approximations in two ways:
The class PEquation from GProp package allows analyzing a collection or cloud of points and verifying if they are coincident, collinear or coplanar within a given precision. If they are, the algorithm computes the mean point, the mean line or the mean plane of the points. If they are not, the algorithm computes the minimal box, which includes all the points.
Packages Geom2dAPI and GeomAPI provide simple methods for approximation and interpolation with minimal programming
The class Interpolate from Geom2dAPI package allows building a constrained 2D BSpline curve, defined by a table of points through which the curve passes. If required, the parameter values and vectors of the tangents can be given for each point in the table.
The class Interpolate from GeomAPI package allows building a constrained 3D BSpline curve, defined by a table of points through which the curve passes. If required, the parameter values and vectors of the tangents can be given for each point in the table.

This class may be instantiated as follows:
From this object, the BSpline curve may be requested as follows:
The class PointsToBSpline from Geom2dAPI package allows building a 2DBSpline curve, which approximates a set of points. You have to define the lowest and highest degree of the curve, its continuity and a tolerance value for it.The tolerance value is used to check that points are not too close to each other, or tangential vectors not too small. The resulting BSpline curve will beC2 or second degree continuous, except where a tangency constraint is defined on a point through which the curve passes. In this case, it will be only C1continuous.
The class PointsToBSpline from GeomAPI package allows building a 3D BSplinecurve, which approximates a set of points. It is necessary to define the lowest and highest degree of the curve, its continuity and tolerance. The tolerance value is used to check that points are not too close to each other,or that tangential vectors are not too small.
The resulting BSpline curve will be C2 or second degree continuous, except where a tangency constraint is defined on a point, through which the curve passes. In this case, it will be only C1 continuous. This class is instantiated as follows:
From this object, the BSpline curve may be requested as follows:
The class PointsToBSplineSurface from GeomAPI package allows building a BSpline surface, which approximates or interpolates a set of points.
Packages AppDef and AppParCurves provide low-level functions, allowing more control over the approximations.
The low-level functions provide a second API with functions to:
You can also find functions to compute:
AppDef package provides low-level tools to allow parallel approximation of groups of points into Bezier or B-Spline curves using multiple point constraints.
The following low level services are provided:

AppParCurves package provides low-level tools to allow parallel approximation of groups of points into Bezier or B-Spline curve with parametric or geometric constraints, such as a requirement for the curve to pass through given points, or to have a given tangency or curvature at a particular point.
The algorithms used include:
The following low-level services are provided:
To approximate a curve with respect to tangency, follow these steps:
Direct Construction methods from gce, GC and GCE2d packages provide simplified algorithms to build elementary geometric entities such as lines, circles and curves. They complement the reference definitions provided by the gp, Geom and Geom2d packages.
The algorithms implemented by gce, GCE2d and GC packages are simple: there is no creation of objects defined by advanced positional constraints (for more information on this subject, see Geom2dGcc and GccAna, which describe geometry by constraints).
For example, to construct a circle from a point and a radius using the gp package, it is necessary to construct axis Ax2d before creating the circle. If gce package is used, and Ox is taken for the axis, it is possible to create a circle directly from a point and a radius.
Another example is the class gce_MakeCirc providing a framework for defining eight problems encountered in the geometric construction of circles and implementing the eight related construction algorithms.
The object created (or implemented) is an algorithm which can be consulted to find out, in particular:
If it was unsuccessful, the status gives the reason for the failure.
In addition, gce, GCE2d and GC each have a Root class. This class is the root of all classes in the package, which return a status. The returned status (successful construction or construction error) is described by the enumeration gce_ErrorType.
Note, that classes, which construct geometric transformations do not return a status, and therefore do not inherit from Root.
The following algorithms used to build entities from gp package are provided by gce package.
Each class from gp package, such as Circ, Circ2d, Mirror, Mirror2d, etc., has the corresponding MakeCirc, MakeCirc2d, MakeMirror, MakeMirror2d, etc. class from gce package.
It is possible to create a point using a gce package class, then question it to recover the corresponding gp object.
This is useful if you are uncertain as to whether the arguments can create the gp object without raising an exception. In the case above, if Point1 and Point2 are closer than the tolerance value required by MakeLin2d, the function Status will return the enumeration gce_ConfusedPoint. This tells you why the gp object cannot be created. If you know that the points Point1 and Point2 are separated by the value exceeding the tolerance value, then you may create the gp object directly, as follows:
GC and GCE2d packages provides an implementation of algorithms used to build entities from Geom and Geom2D packages. They implement the same algorithms as the gce package, and also contain algorithms for trimmed surfaces and curves. The following algorithms are available:
Each class from GCE2d package, such as Circle, Ellipse, Mirror, etc., has the corresponding MakeCircle, MakeEllipse, MakeMirror, etc. class from Geom2d package. Besides, the class MakeArcOfCircle returns an object of type TrimmedCurve from Geom2d.
Each class from GC package, such as Circle, Ellipse, Mirror, etc., has the corresponding MakeCircle, MakeEllipse, MakeMirror, etc. class from Geom package. The following classes return objects of type TrimmedCurve from Geom:
The Conversion to and from BSplines component has two distinct purposes:
The "Conversion to and from BSplines" component is composed of three packages.
The Convert package provides algorithms to convert the following into a BSpline curve or surface:
These algorithms compute the data needed to define the resulting BSpline curve or surface. This elementary data (degrees, periodic characteristics, poles and weights, knots and multiplicities) may then be used directly in an algorithm, or can be used to construct the curve or the surface by calling the appropriate constructor provided by the classes Geom2d_BSplineCurve, Geom_BSplineCurve or Geom_BSplineSurface.
The Geom2dConvert package provides the following:
The GeomConvert package also provides the following:
The Points on Curves component comprises high level functions providing an API for complex algorithms that compute points on a 2D or 3D curve.
The following characteristic points exist on parameterized curves in 3d space:
GCPnts package provides algorithms to calculate such points:
Let us take an adapted curve C, i.e. an object which is an interface between the services provided by either a 2D curve from the package Geom2d (in case of an Adaptor_Curve2d curve) or a 3D curve from the package Geom (in case of an Adaptor_Curve curve), and the services required on the curve by the computation algorithm. The adapted curve is created in the following way:
2D case:
3D case:
The algorithm is then constructed with this object:
The classes to calculate the minimum distance between points, curves, and surfaces in 2d and 3d are provided by GeomAPI and Geom2dAPI packages.
These packages calculate the extrema of distance between:
The GeomAPI_ProjectPointOnCurve class allows calculation of all extrema between a point and a curve. Extrema are the lengths of the segments orthogonal to the curve. The GeomAPI_ProjectPointOnSurface class allows calculation of all extrema between a point and a surface. Extrema are the lengths of the segments orthogonal to the surface. These classes use the "Projection" criteria for optimization.
The Geom2dAPI_ExtremaCurveCurve class allows calculation of all minimal distances between two 2D geometric curves. The GeomAPI_ExtremaCurveCurve class allows calculation of all minimal distances between two 3D geometric curves. These classes use Euclidean distance as the criteria for optimization.
The GeomAPI_ExtremaCurveSurface class allows calculation of one extrema between a 3D curve and a surface. Extrema are the lengths of the segments orthogonal to the curve and the surface. This class uses the "Projection" criteria for optimization.
The GeomAPI_ExtremaSurfaceSurface class allows calculation of one minimal and one maximal distance between two surfaces. This class uses Euclidean distance to compute the minimum, and "Projection" criteria to compute the maximum.
Geom2d package defines geometric objects in 2dspace. All geometric entities are STEP processed. The objects are handled by reference.
In particular, Geom2d package provides classes for:
The following objects are available:
Before creating a geometric object, it is necessary to decide how the object is handled. The objects provided by Geom2d package are handled by reference rather than by value. Copying an instance copies the handle, not the object, so that a change to one instance is reflected in each occurrence of it. If a set of object instances is needed rather than a single object instance, TColGeom2d package can be used. This package provides standard and frequently used instantiations of one-dimensional arrays and sequences for curves from Geom2d package. All objects are available in two versions:
The key characteristic of Geom2d curves is that they are parameterized. Each class provides functions to work with the parametric equation of the curve, and, in particular, to compute the point of parameter u on a curve and the derivative vectors of order 1, 2.., N at this point.
As a consequence of the parameterization, a Geom2d curve is naturally oriented.
Parameterization and orientation differentiate elementary Geom2dcurves from their equivalent as provided by gp package. Geom2d package provides conversion functions to transform a Geom2d object into a gp object, and vice-versa, when this is possible.
Moreover, Geom2d package provides more complex curves, including Bezier curves, BSpline curves, trimmed curves and offset curves.
Geom2d objects are organized according to an inheritance structure over several levels.
Thus, an ellipse (specific class Geom2d_Ellipse) is also a conical curve and inherits from the abstract class Geom2d_Conic, while a Bezier curve (concrete class Geom2d_BezierCurve) is also a bounded curve and inherits from the abstract class Geom2d_BoundedCurve; both these examples are also curves (abstract class Geom2d_Curve). Curves, points and vectors inherit from the abstract class Geom2d_Geometry, which describes the properties common to any geometric object from the Geom2d package.
This inheritance structure is open and it is possible to describe new objects, which inherit from those provided in the Geom2d package, provided that they respect the behavior of the classes from which they are to inherit.
Finally, Geom2d objects can be shared within more complex data structures. This is why they are used within topological data structures, for example.
Geom2d package uses the services of the gp package to:
However, the Geom2d package essentially provides data structures and not algorithms. You can refer to the GCE2d package to find more evolved construction algorithms for Geom2d objects.
The Geom package defines geometric objects in 3d space and contains all basic geometric transformations, such as identity, rotation, translation, mirroring, scale transformations, combinations of transformations, etc. as well as special functions depending on the reference definition of the geometric object (e.g. addition of a control point on a B-Spline curve,modification of a curve, etc.). All geometrical entities are STEP processed.
In particular, it provides classes for:
The following objects are available:
The key characteristic of Geom curves and surfaces is that they are parameterized. Each class provides functions to work with the parametric equation of the curve or surface, and, in particular, to compute:
As a consequence of this parameterization, a Geom curve or surface is naturally oriented.
Parameterization and orientation differentiate elementary Geom curves and surfaces from the classes of the same (or similar) names found in gp package. Geom package also provides conversion functions to transform a Geom object into a gp object, and vice-versa, when such transformation is possible.
Moreover, Geom package provides more complex curves and surfaces, including:
Geom objects are organized according to an inheritance structure over several levels. Thus, a sphere (concrete class Geom_SphericalSurface) is also an elementary surface and inherits from the abstract class Geom_ElementarySurface, while a Bezier surface (concrete class Geom_BezierSurface) is also a bounded surface and inherits from the abstract class Geom_BoundedSurface; both these examples are also surfaces (abstract class Geom_Surface). Curves, points and vectors inherit from the abstract class Geom_Geometry, which describes the properties common to any geometric object from the Geom package.
This inheritance structure is open and it is possible to describe new objects, which inherit from those provided in the Geom package, on the condition that they respect the behavior of the classes from which they are to inherit.
Finally, Geom objects can be shared within more complex data structures. This is why they are used within topological data structures, for example.
If a set of object instances is needed rather than a single object instance, TColGeom package can be used. This package provides instantiations of one- and two-dimensional arrays and sequences for curves from Geom package. All objects are available in two versions:
The Geom package uses the services of the gp package to:
However, the Geom package essentially provides data structures, not algorithms.
You can refer to the GC package to find more evolved construction algorithms for Geom objects.
OCCT Topology allows accessing and manipulating data of objects without dealing with their 2D or 3D representations. Whereas OCCT Geometry provides a description of objects in terms of coordinates or parametric values, Topology describes data structures of objects in parametric space. These descriptions use location in and restriction of parts of this space.
Topological library allows you to build pure topological data structures. Topology defines relationships between simple geometric entities. In this way, you can model complex shapes as assemblies of simpler entities. Due to a built-in non-manifold (or mixed-dimensional) feature, you can build models mixing:
You can, for example, represent a single object made of several distinct bodies containing embedded curves and surfaces connected or non-connected to an outer boundary.
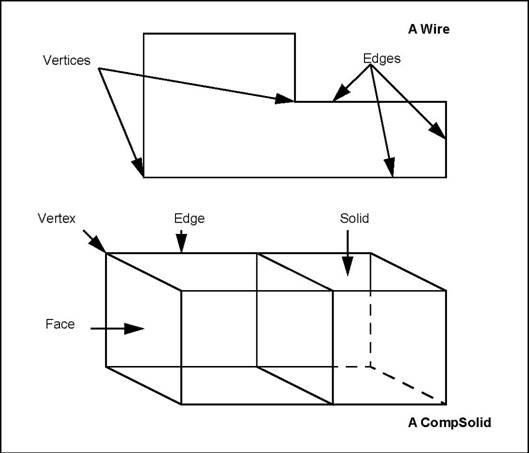
Abstract topological data structure describes a basic entity – a shape, which can be divided into the following component topologies:
The wire and the solid can be either infinite or closed.
A face with 3D underlying geometry may also refer to a collection of connected triangles that approximate the underlying surface. The surfaces can be undefined leaving the faces represented by triangles only. If so, the model is purely polyhedral.
Topology defines the relationship between simple geometric entities, which can thus be linked together to represent complex shapes.
Abstract Topology is provided by six packages. The first three packages describe the topological data structure used in Open CASCADE Technology:
Three additional packages provide tools to access and manipulate this abstract topology:
The TopAbs package provides general enumerations describing the basic concepts of topology and methods to handle these enumerations. It contains no classes. This package has been separated from the rest of the topology because the notions it contains are sufficiently general to be used by all topological tools. This avoids redefinition of enumerations by remaining independent of modeling resources. The TopAbs package defines three notions:
TopAbs contains the TopAbs_ShapeEnum enumeration, which lists the different topological types:
A topological model can be considered as a graph of objects with adjacency relationships. When modeling a part in 2D or 3D space it must belong to one of the categories listed in the ShapeEnum enumeration. The TopAbspackage lists all the objects, which can be found in any model. It cannot be extended but a subset can be used. For example, the notion of solid is useless in 2D.
The terms of the enumeration appear in order from the most complex to the most simple, because objects can contain simpler objects in their description. For example, a face references its wires, edges, and vertices.
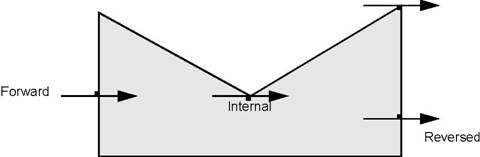
The notion of orientation is represented by the TopAbs_Orientation enumeration. Orientation is a generalized notion of the sense of direction found in various modelers. This is used when a shape limits a geometric domain; and is closely linked to the notion of boundary. The three cases are the following:
In each case the topological form used as the boundary of a geometric domain of a higher dimension defines two local regions of which one is arbitrarily considered as the default region.
For a curve limited by a vertex the default region is the set of points with parameters greater than the vertex. That is to say it is the part of the curve after the vertex following the natural direction along the curve.
For a surface limited by an edge the default region is on the left of the edge following its natural direction. More precisely it is the region pointed to by the vector product of the normal vector to the surface and the vector tangent to the curve.
For a space limited by a face the default region is found on the negative side of the normal to the surface.
Based on this default region the orientation allows definition of the region to be kept, which is called the interior or material. There are four orientations defining the interior.
| Orientation | Description |
|---|---|
| FORWARD | The interior is the default region. |
| REVERSED | The interior is the region complementary to the default. |
| INTERNAL | The interior includes both regions. The boundary lies inside the material. For example a surface inside a solid. |
| EXTERNAL | The interior includes neither region. The boundary lies outside the material. For example an edge in a wire-frame model. |

The notion of orientation is a very general one, and it can be used in any context where regions or boundaries appear. Thus, for example, when describing the intersection of an edge and a contour it is possible to describe not only the vertex of intersection but also how the edge crosses the contour considering it as a boundary. The edge would therefore be divided into two regions: exterior and interior and the intersection vertex would be the boundary. Thus an orientation can be associated with an intersection vertex as in the following figure:
| Orientation | Association |
|---|---|
| FORWARD | Entering |
| REVERSED | Exiting |
| INTERNAL | Touching from inside |
| EXTERNAL | Touching from outside |
Along with the Orientation enumeration the TopAbs package defines four methods:
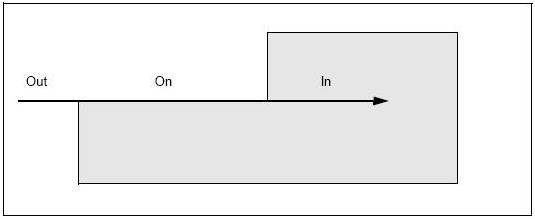
The TopAbs_State enumeration described the position of a vertex or a set of vertices with respect to a region. There are four terms:
| Position | Description |
|---|---|
| IN | The point is interior. |
| OUT | The point is exterior. |
| ON | The point is on the boundary(within tolerance). |
| UNKNOWN | The state of the point is indeterminate. |
The UNKNOWN term has been introduced because this enumeration is often used to express the result of a calculation, which can fail. This term can be used when it is impossible to know if a point is inside or outside, which is the case with an open wire or face.

The State enumeration can also be used to specify various parts of an object. The following figure shows the parts of an edge intersecting a face.
A local coordinate system can be viewed as either of the following:
TopLoc package distinguishes two notions:
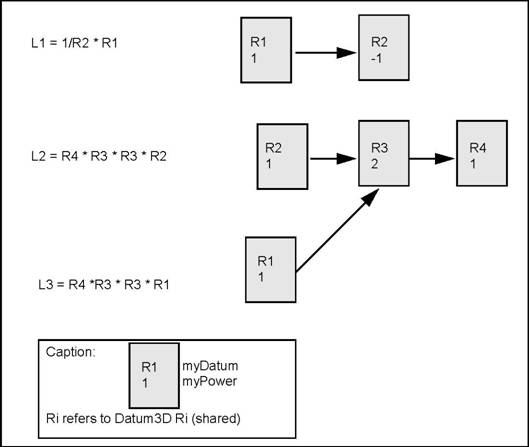
Two reference coordinates are equal if they are made up of the same elementary coordinates in the same order. There is no numerical comparison. Two coordinates can thus correspond to the same transformation without being equal if they were not built from the same elementary coordinates.
For example, consider three elementary coordinates:
The composite coordinates are:
NOTE C3 and C4 are equal because they are both R1 * R2 * R3.
The TopLoc package is chiefly targeted at the topological data structure, but it can be used for other purposes.
TopLoc_Datum3D class represents a change of elementary coordinates. Such changes must be shared so this class inherits from Standard_Transient. The coordinate is represented by a transformation gp_Trsfpackage. This transformation has no scaling factor.
The TopoDS package describes the topological data structure with the following characteristics:
As stated above, OCCT Topology describes data structures of objects in parametric space. These descriptions use localization in and restriction of parts of this space. The types of shapes, which can be described in these terms, are the vertex, the face and the shape. The vertex is defined in terms of localization in parametric space, and the face and shape, in terms of restriction of this space.
OCCT topological descriptions also allow the simple shapes defined in these terms to be combined into sets. For example, a set of edges forms a wire; a set of faces forms a shell, and a set of solids forms a composite solid (CompSolid in Open CASCADE Technology). You can also combine shapes of either sort into compounds. Finally, you can give a shape an orientation and a location.
Listing shapes in order of complexity from vertex to composite solid leads us to the notion of the data structure as knowledge of how to break a shape down into a set of simpler shapes. This is in fact, the purpose of the TopoDS package.
The model of a shape is a shareable data structure because it can be used by other shapes (an edge can be used by more than one face of a solid). A shareable data structure is handled by reference. When a simple reference is insufficient, two pieces of information are added: an orientation and a local coordinate reference.
The TopoDS_TShape class is the root of all shape descriptions. It contains a list of shapes. Classes inheriting TopoDS_TShape can carry the description of a geometric domain if necessary (for example, a geometric point associated with a TVertex). A TopoDS_TShape is a description of a shape in its definition frame of reference. This class is manipulated by reference.
The TopoDS_Shape class describes a reference to a shape. It contains a reference to an underlying abstract shape, an orientation, and a local reference coordinate. This class is manipulated by value and thus cannot be shared.
The class representing the underlying abstract shape is never referenced directly. The TopoDS_Shape class is always used to refer to it.
The information specific to each shape (the geometric support) is always added by inheritance to classes deriving from TopoDS_TShape. The following figures show the example of a shell formed from two faces connected by an edge.

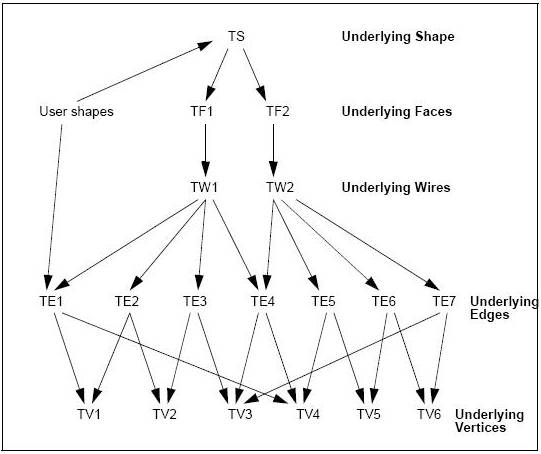
In the previous diagram, the shell is described by the underlying shape TS, and the faces by TF1 and TF2. There are seven edges from TE1 to TE7 and six vertices from TV1 to TV6.
The wire TW1 references the edges from TE1 to TE4; TW2 references from TE4 to TE7.
The vertices are referenced by the edges as follows:TE1(TV1,TV4), TE2(TV1,TV2), TE3(TV2,TV3), TE4(TV3,TV4), TE5(TV4,TV5), TE6(T5,TV6),TE7(TV3,TV6).
Note that this data structure does not contain any back references. All references go from more complex underlying shapes to less complex ones. The techniques used to access the information are described later. The data structure is as compact as possible. Sub-objects can be shared among different objects.
Two very similar objects, perhaps two versions of the same object, might share identical sub-objects. The usage of local coordinates in the data structure allows the description of a repetitive sub-structure to be shared.
The compact data structure avoids the loss of information associated with copy operations which are usually used in creating a new version of an object or when applying a coordinate change.
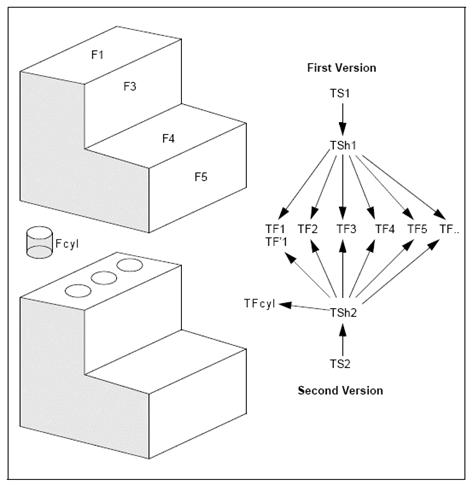
The following figure shows a data structure containing two versions of a solid. The second version presents a series of identical holes bored at different positions. The data structure is compact and yet keeps all information on the sub-elements.
The three references from TSh2 to the underlying face TFcyl have associated local coordinate systems, which correspond to the successive positions of the hole.
TopoDS is based on class TopoDS_Shape and the class defining its underlying shape. This has certain advantages, but the major drawback is that these classes are too general. Different shapes they could represent do not type them (Vertex, Edge, etc.) hence it is impossible to introduce checks to avoid incoherences such as inserting a face in an edge.
TopoDS package offers two sets of classes, one set inheriting the underlying shape with neither orientation nor location and the other inheriting TopoDS_Shape, which represent the standard topological shapes enumerated in TopAbs package.
The following classes inherit Shape: TopoDS_Vertex, TopoDS_Edge, TopoDS_Wire, TopoDS_Face, TopoDS_Shell, TopoDS_Solid, TopoDS_CompSolid, and TopoDS_Compound. In spite of the similarity of names with those inheriting from TopoDS_TShape there is a profound difference in the way they are used.
TopoDS_Shape class and the classes, which inherit from it, are the natural means to manipulate topological objects. TopoDS_TShape classes are hidden. TopoDS_TShape describes a class in its original local coordinate system without orientation. TopoDS_Shape is a reference to TopoDS_TShape with an orientation and a local reference.
TopoDS_TShape class is deferred; TopoDS_Shape class is not. Using TopoDS_Shape class allows manipulation of topological objects without knowing their type. It is a generic form. Purely topological algorithms often use the TopoDS_Shape class.
TopoDS_TShape class is manipulated by reference; TopoDS_Shape class by value. A TopoDS_Shape is nothing more than a reference enhanced with an orientation and a local coordinate. The sharing of TopoDS_Shapes is meaningless. What is important is the sharing of the underlying TopoDS_TShapes. Assignment or passage in argument does not copy the data structure: this only creates new TopoDS_Shapes which refer to the same TopoDS_TShape.
Although classes inheriting TopoDS_TShape are used for adding extra information, extra fields should not be added in a class inheriting from TopoDS_Shape. Classes inheriting from TopoDS_Shape serve only to specialize a reference in order to benefit from static type control (carried out by the compiler). For example, a routine that receives a TopoDS_Face in argument is more precise for the compiler than the one, which receives a TopoDS_Shape. It is pointless to derive other classes than those found in TopoDS. All references to a topological data structure are made with the Shape class and its inheritors defined in TopoDS.
There are no constructors for the classes inheriting from the TopoDS_Shape class, otherwise the type control would disappear through implicit casting (a characteristic of C++). The TopoDS package provides package methods for casting an object of the TopoDS_Shape class in one of these sub-classes, with type verification.
The following example shows a routine receiving an argument of the TopoDS_Shape type, then putting it into a variable V if it is a vertex or calling the method ProcessEdge if it is an edge.
The TopExp package provides tools for exploring the data structure described with the TopoDS package. Exploring a topological structure means finding all sub-objects of a given type, for example, finding all the faces of a solid.
The TopExp package provides the class TopExp_Explorer to find all sub-objects of a given type. An explorer is built with:
The Explorer visits the whole structure in order to find the shapes of the requested type not contained in the type to avoid. The example below shows how to find all faces in the shape S:
Find all the vertices which are not in an edge
Find all the faces in a SHELL, then all the faces not in a SHELL:
The Explorer presumes that objects contain only objects of an equal or inferior type. For example, if searching for faces it does not look at wires, edges, or vertices to see if they contain faces.
The MapShapes method from TopExp package allows filling a Map. An exploration using the Explorer class can visit an object more than once if it is referenced more than once. For example, an edge of a solid is generally referenced by two faces. To process objects only once, they have to be placed in a Map.
Example
In the following example all faces and all edges of an object are drawn in accordance with the following rules:
The following steps are performed:
TopTools package contains tools for exploiting the TopoDS data structure. It is an instantiation of the tools from TCollection package with the Shape classes of TopoDS.
With a TopTools_Map, a set of references to Shapes can be kept without duplication. The following example counts the size of a data structure as a number of TShapes.
This program is incorrect if there is sharing in the data structure.
Thus for a contour of four edges it should count 1 wire + 4 edges +4 vertices with the result 9, but as the vertices are each shared by two edges this program will return 13. One solution is to put all the Shapes in a Map so as to avoid counting them twice, as in the following example:
Note For more details about Maps, refer to the TCollection documentation (Foundation Classes Reference Manual).
The following example is more ambitious and writes a program which copies a data structure using an IndexedMap. The copy is an identical structure but it shares nothing with the original. The principal algorithm is as follows:
In the above example, the index i is that of the first object not treated in the Map. When i reaches the same size as the Map this means that everything has been treated. The treatment consists in inserting in the Map all the sub-objects, if they are not yet in the Map, they are inserted with an index greater than i.
Note that the objects are inserted with a local reference set to the identity and a FORWARD orientation. Only the underlying TShape is of great interest.
Below is the auxiliary function, which copies the element of rank i from the map to the table. This method checks if the object has been copied; if not copied, then an empty copy is performed into the table and the copies of all the sub-elements are inserted by finding their rank in the map.
Wire Explorer
BRepTools_WireExplorer class can access edges of a wire in their order of connection.
For example, in the wire in the image we want to recuperate the edges in the order {e1, e2, e3,e4, e5}:

TopExp_Explorer, however, recuperates the lines in any order.
BRepLProp package provides the Local Properties of Shapes component, which contains algorithms computing various local properties on edges and faces in a BRep model.
The local properties which may be queried are:
Analyzed edges and faces are described as BRepAdaptor curves and surfaces, which provide shapes with an interface for the description of their geometric support. The base point for local properties is defined by its u parameter value on a curve, or its (u, v) parameter values on a surface.
The "Local Properties of Curves and Surfaces" component provides algorithms for computing various local properties on a Geom curve (in 2D or 3D space) or a surface. It is composed of:
Curves are either Geom_Curve curves (in 3D space) or Geom2d_Curve curves (in the plane). Surfaces are Geom_Surface surfaces. The point on which local properties are calculated is defined by its u parameter value on a curve, and its (u,v) parameter values on a surface.
It is possible to query the same local properties for points as mentioned above, and additionally for 2D curves:
To check the concavity of a surface, proceed as follows:
Types of supported continuities for curves and surfaces are described in GeomAbs_Shape enumeration.
In respect of curves, the following types of continuity are supported (see the figure below):
Note: Geometric continuity (G1, G2) means that the curve can be reparametrized to have parametric (C1, C2) continuity.
The following types of surface continuity are supported:
Against single surface, the connection of two surfaces (see the figure above) defines its continuity in each intersection point only. Smoothness of connection is a minimal value of continuities on the intersection curve.
Regularity of an edge is a smoothness of connection of two faces sharing this edge. In other words, regularity is a minimal continuity between connected faces in each point on edge.
Edge's regularity can be set by BRep_Builder::Continuity method. To get the regularity use BRep_Tool::Continuity method.
Some algorithms like Fillet set regularity of produced edges by their own algorithms. On the other hand, some other algorithms (like Boolean Operations, Shape Healing, etc.) do not set regularity. If the regularity is needed to be set correctly on a shape, the method BRepLib::EncodeRegularity can be used. It calculates and sets correct values for all edges of the shape.
The regularity flag is extensively used by the following high level algorithms: Chamfer, Draft Angle, Hidden Line Removal, Gluer.
The Global Properties of Shapes component provides algorithms for computing the global properties of a composite geometric system in 3D space, and frameworks to query the computed results.
The global properties computed for a system are:
Geometric systems are generally defined as shapes. Depending on the way they are analyzed, these shapes will give properties of:
The global properties of several systems may be brought together to give the global properties of the system composed of the sum of all individual systems.
The Global Properties of Shapes component is composed of:
Packages GeomLProp and Geom2dLProp provide algorithms calculating the local properties of curves and surfaces
A curve (for one parameter) has the following local properties:
A surface (for two parameters U and V) has the following local properties:
The following methods are available:
Note that the B-spline curve and surface are accepted but they are not cut into pieces of the desired continuity. It is the global continuity, which is seen.
Some Open CASCADE Technology general algorithms may work theoretically on numerous types of curves or surfaces.
To do this, they simply get the services required of the analyzed curve or surface through an interface so as to a single API, whatever the type of curve or surface. These interfaces are called adaptors.
For example, Adaptor3d_Curve is the abstract class which provides the required services by an algorithm which uses any 3d curve.
GeomAdaptor package provides interfaces:
Geom2dAdaptor package provides interfaces:
BRepAdaptor package provides interfaces:
When you write an algorithm which operates on geometric objects, use Adaptor3d (or Adaptor2d) objects.
As a result, you can use the algorithm with any kind of object, if you provide for this object an interface derived from Adaptor3d or Adaptor2d. These interfaces are easy to use: simply create an adapted curve or surface from a Geom2d curve, and then use this adapted curve as an argument for the algorithm? which requires it.
Bounding boxes are used in many OCCT algorithms. The most common use is as a filter avoiding check of excess interferences between pairs of shapes (check of interferences between bounding boxes is much simpler then between shapes and if they do not interfere then there is no point in searching interferences between the corresponding shapes). Generally, bounding boxes can be divided into two main types:
The image below illustrates the example, when using OBB is better than AABB.
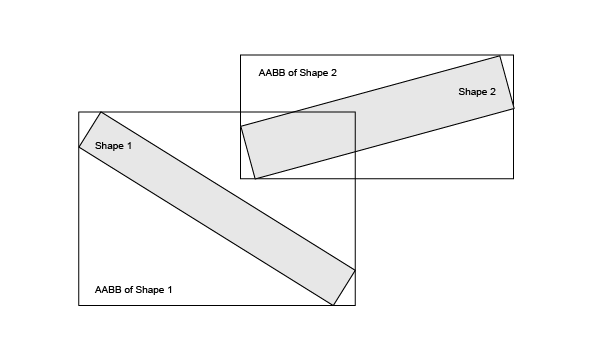
AABBs in this picture are interfered. Therefore, many OCCT algorithms will spend much time to interfere the shapes. However, if we check OBBs, which are not interfered, then searching of interferences between the shapes will not be necessary. At that, creation and analysis of OBBs takes significantly more time than the analogical operations with AABB.
Later in this section, the bounding boxes having the smallest surface area will be called optimal.
In OCCT, bounding boxes are defined in Bnd package. Bnd_Box class defines AABB, Bnd_OBB class defines OBB. These classes contain the following common methods (this list is not complete; see the documentation about the corresponding class for detailed information):
BRepBndLib class contains methods for creation of bounding boxes (both AABB and OBB) from the shapes.
The algorithm is described in "Fast Computation of Tight Fitting Oriented Bounding Boxes" by Thomas Larsson and Linus Källberg (FastOBBs.pdf). It includes the following steps:
1. Choose \( N_{a} (N_{a} \geq 3) \) initial axes.
2. Project every given point to the every chosen (in item 1) axis. At that, "minimal" and "maximal" points of every axis (i.e. point having minimal and maximal parameter (correspondingly) of the projection to this axis) are chosen. I.e. \( 2*N_{a} \) points will be held and this set can contain equal points. Later (unless otherwise specified) in this algorithm we will work with these \( 2*N_{a} \) points only.
3. Choose one pair of points among all pairs of "minimal" and "maximal" points of every axis (from item 1), with two furthest points. Let \( p_{0} \) and \( p_{1} \) be the "minimal" and "maximal" point of this pair.
4. Create an axis \( \mathbf{e_{0}}\left \{ \overrightarrow{p_{0}p_{1}} \right \} \) (i.e. having direction \( \overrightarrow{p_{0}p_{1}} \) ).
5. Choose the point \( p_{2} \) (from the set defined in item 2) which is in the maximal distance from the infinite line directed along \( \mathbf{e_{0}} \) axis.
Further, let us consider the triangle \( T_{0}\left \langle p_{0}, p_{1}, p_{2} \right \rangle \) (i.e. having vertices \( p_{0}, p_{1} \) and \( p_{2} \)). Namely:
6. Create new axes: \( \mathbf{e_{1}}\left \{ \overrightarrow{p_{1}p_{2}} \right \} \), \( \mathbf{e_{2}}\left \{ \overrightarrow{p_{2}p_{0}} \right \} \), \( \mathbf{n}\left \{ \overrightarrow{\mathbf{e_{0}}} \times \overrightarrow{\mathbf{e_{1}}} \right \} \), \( \mathbf{m_{0}}\left \{ \overrightarrow{\mathbf{e_{0}}} \times \overrightarrow{\mathbf{n}} \right \} \), \( \mathbf{m_{1}}\left \{ \overrightarrow{\mathbf{e_{1}}} \times \overrightarrow{\mathbf{n}} \right \} \), \( \mathbf{m_{2}}\left \{ \overrightarrow{\mathbf{e_{2}}} \times \overrightarrow{\mathbf{n}} \right \} \).
7. Create OBBs based on the following axis: \( \left \{ \mathbf{e_{0}} \vdots \mathbf{m_{0}} \vdots \mathbf{n} \right \} \), \( \left \{ \mathbf{e_{1}} \vdots \mathbf{m_{1}} \vdots \mathbf{n} \right \} \) and \( \left \{ \mathbf{e_{2}} \vdots \mathbf{m_{2}} \vdots \mathbf{n} \right \} \) . Choose optimal OBB.
8. Choose the points \( q_{0} \) and \( q_{1} \) (from the set defined in item 2), which are in maximal distance from the plane of the triangle \( T_{0} \) (from both sides of this plane). At that, \( q_{0} \) has minimal coordinate along the axis \( \mathbf{n} \), \( q_{1} \) has a maximal coordinate.
9. Repeat the step 6...7 for the triangles \( T_{1}\left \langle p_{0}, p_{1}, q_{0} \right \rangle \), \( T_{2}\left \langle p_{1}, p_{2}, q_{0} \right \rangle \), \( T_{3}\left \langle p_{0}, p_{2}, q_{0} \right \rangle \), \( T_{4}\left \langle p_{0}, p_{1}, q_{1} \right \rangle \), \( T_{5}\left \langle p_{1}, p_{2}, q_{1} \right \rangle \), \( T_{6}\left \langle p_{0}, p_{2}, q_{1} \right \rangle \).
10. Compute the center of OBB and its half dimensions.
11. Create OBB using the center, axes and half dimensions.
For creation of the optimal OBB from set of points the same algorithm as described above is used but with some simplifications in logic and increased computation time. For the optimal OBB it is necessary to check all possible axes which can be created by the extremal points. And since the extremal points are only valid for the initial axes it is necessary to project the whole set of points on each axis. This approach usually provides much tighter OBB but the performance is lower. The complexity of the algorithm is still linear and with use of BVH for the set of points it is O(N + C*log(N)).
Here is the example of optimal and not optimal OBB for the model using the set of 125K nodes:
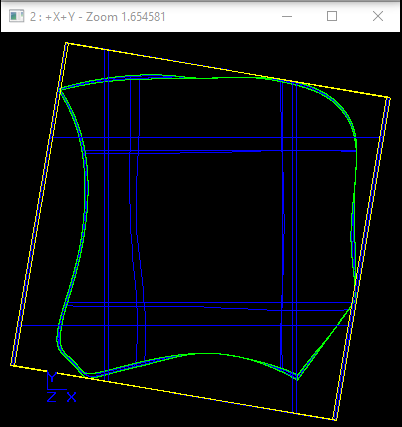
Not optimal OBB by DiTo-14 | 
Optimal OBB by DiTo-14 | 
Not optimal OBB by PCA |
Computation of the not optimal OBB in this case took 0.007 sec, optimal - 0.1 sec, which is about 14 times slower. Such performance is comparable to creation of the OBB for this shape by PCA approach (see below) which takes about 0.17 sec.
The computation of optimal OBB is controlled by the same theIsOptimal flag in the BRepBndLib::AddOBB method as for PCA algorithm.
These algorithms are implemented in the Bnd_OBB::ReBuild(...) method.
The algorithm contains the following steps:
According to the "Separating Axis Theorem for Oriented Bounding Boxes", it is necessary to check the 15 separating axes: 6 axes of the boxes and 9 are their cross products.
The algorithm of analyzing axis \( \mathbf{l} \) is following:
If OBBs are not interfered in terms of at least one axis (of 15) then they are not interfered at all.
Create a new OBB (see the section Creation of OBB from set of points) based on the source point and all vertices of the given bounding boxes.
Method BRepBndLib::AddOBB(...) allows creating the bounding box from a complex object (TopoDS_Shape). This method uses both algorithms described in the sections Creation of OBB from set of points and sections Creation of OBB based on Axes of inertia.
The first algorithm is used if the outer shell of the shape can be represented by a set of points contained in it. Namely, only the following elements are the source of set of points:
If the required set of points cannot be extracted then the algorithm from section Creation of OBB based on Axes of inertia is used for OBB creation.
The package BRepBndLib contains methods BRepBndLib::Add(...), BRepBndLib::AddClose(...) and BRepBndLib::AddOptimal(...) for creation of AABB of a shape. See the reference manual for the detailed information.