
Mon, 07/03/2017 - 17:43
The version 7.0 of Open CASCADE Technology features the new General Fuse (GF) based algorithm - Cells Builder. The algorithm can be very useful if you have to perform several standard Boolean operations such as CUT, COMMON and FUSE on the same shapes to obtain the final result.
Due to the possibility to get any split parts of the arguments (parts of the input shapes split in the places of intersection with other input shapes), which are called Cells (that’s where the name for the algorithm comes from), the Cells Builder may significantly simplify and speed up these operations as all intersections will be performed in a single run. In effect, the Cells Builder allows executing the Boolean expressions on the shapes, i.e. performing a sequence of standard Boolean operations in one operation.
The first version of the algorithm (available since OCCT 7.0) had limited capabilities. It worked only with the shapes of the same dimension - only VERTICES, or only EDGES, etc. Recently, the algorithm has been extended to also work with multi-dimensional input shapes. The next version of Open CASCADE (7.2) will feature this extension.
Application
The Cells Builder algorithm has a very wide application - from building the result of General Fuse and any Boolean operations to building the result of your own application-specific operation. Cells Builder extends the idea of General Fuse algorithm by providing the means to specify uniquely any cell (split part of the arguments) to be taken into the result. The result of General Fuse is a collection of all split parts of all arguments. See the example of three circular faces C1(red), C2(green) and C3 (blue) on the image below:
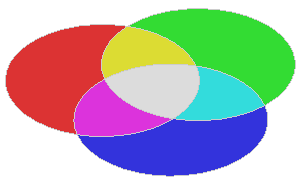
Most often, however, you need to take into the result the split parts of only some of the arguments (as an example of partition operation):
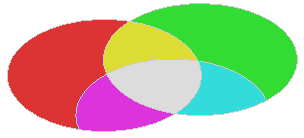
Sometimes the split parts of one argument should be taken and the splits of other shapes should be avoided, and then vice versa:

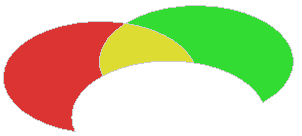
Or may be you need to take into the result only the parts of arguments not contained in any other argument:

Using the Cells Builder allows getting all these results of Boolean Expressions in one operation. As you can see the Cells Builder can also be useful when you need to perform many different Boolean operations on the same input shapes. For instance, you need to cut the material from the object and to get the part that has been removed, i.e. you need to perform two subsequent operations CUT and then COMMON, or, as in Case 3 of Gluing options, you need to CUT the two objects and then to FUSE the result with the tool. Even for these simple operations using the Cells Builder will be beneficial. The Cells Builder improves the performance by avoiding constant rebuilding of the splits of the arguments as it is done in Boolean operations. All splits are built only once and then reused for getting the new results. Such approach allows both saving time and adding robustness to the whole process. Another useful feature of the algorithm is the possibility to remove any internal boundaries between splits. In other words it gives the possibility to fuse any parts added to the result and to keep any other parts separate. For that, the approach with materials IDs has been implemented. When you add cells into the result, you can set the material for each cell, and the boundaries between cells with the same material will be removed:

Note that the internal boundaries between parts of different dimensions will not be removed. Thus the result of the algorithm can be finely tuned by appropriate assignment of material IDs.. Additionally there is a possibility to produce containers from the parts added into the result (Wires, Shells, Compsolids), even if the arguments are not containers.
Usage
The usage of the algorithm is fully described in the OCCT on-line documentation - Cells Builder algorithm description.
Examples
1. Same-dimensional arguments
The following simple example demonstrates the usage and possibilities of the algorithm on three spheres:
psphere s1 15 psphere s2 15 psphere s3 15 ttranslate s1 0 0 10 ttranslate s2 20 0 10 ttranslate s3 10 0 0 bclearobjects; bcleartools baddobjects s1 s2 s3 bfillds bcbuild rx
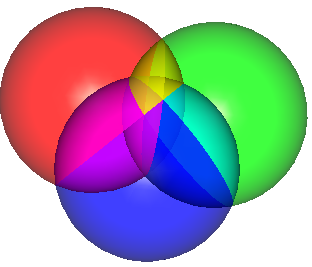
| Example | Usage | Image of the result |
| Getting common of all three spheres | API: aLSToTake.Clear(); aLSToTake.Append(aS1); aLSToTake.Append(aS2); aLSToTake.Append(aS3); aLSToAvoid.Clear(); aCBuilder.AddToResult (aLSToTake,aLSToAvoid); DRAW: bcremoveall bcadd res s1 1 s2 1 s3 1 |  |
| Getting all splits except for the common | API: aLSToAvoid.Clear(); aLSToTake.Clear(); aLSToTake.Append(aS1); aCBuilder.AddToResult (aLSToTake,aLSToAvoid); aLSToTake.Clear(); aLSToTake.Append(aS2); aCBuilder.AddToResult (aLSToTake,aLSToAvoid); aLSToTake.Clear(); aLSToTake.Append(aS3); aCBuilder.AddToResult (aLSToTake,aLSToAvoid); aLSToTake.Clear(); aLSToTake.Append(aS1); aLSToTake.Append(aS2); aLSToTake.Append(aS3); aCBuilder.RemoveFromResult (aLSToTake,aLSToAvoid); DRAW: bcremoveall bcadd res s1 1 bcadd res s2 1 bcadd res s3 1 bcremove res s1 1 s2 1 s3 1 |  |
| Getting splits of the first sphere contained in other spheres | API: aLSToAvoid.Clear(); aLSToTake.Clear(); aLSToTake.Append(aS1); aLSToTake.Append(aS2); aCBuilder.AddToResult (aLSToTake,aLSToAvoid); aLSToTake.Clear(); aLSToTake.Append(aS1); aLSToTake.Append(aS3); aCBuilder.AddToResult (aLSToTake,aLSToAvoid); DRAW: bcremoveall bcadd res s1 1 s2 1 bcadd res s1 1 s3 1 |  |
| Getting splits of the first sphere contained in the second sphere but not contained in the third one | API: aLSToAvoid.Clear(); aLSToTake.Clear(); aLSToTake.Append(aS1); aLSToTake.Append(aS2); aLSToAvoid.Append(aS3); aCBuilder.AddToResult (aLSToTake,aLSToAvoid); DRAW: bcremoveall bcadd res s1 1 s2 1 s3 0 |  |
| Getting splits of the first and the second spheres not contained in the third one, and removing boundaries between splits of the second sphere | API: aLSToAvoid.Clear(); aLSToTake.Clear(); aLSToTake.Append(aS1); aLSToAvoid.Append(aS3); aCBuilder.AddToResult (aLSToTake,aLSToAvoid); aLSToAvoid.Clear(); aLSToTake.Clear(); aLSToTake.Append(aS2); aLSToAvoid.Append(aS3); iMaterial = 1; aCBuilder.AddToResult (aLSToTake,aLSToAvoid, iMaterial); aCBuilder.RemoveInternalBoundaries(); DRAW: bcremoveall bcadd res s1 1 s3 0 bcadd res s2 1 s3 0 -m 1 bcremoveint res |  |
| Getting all splits. Fusing splits of the first sphere together and Fusing splits of the second and the third sphere not contained in the first one. | API: aLSToAvoid.Clear(); aLSToTake.Clear(); aLSToTake.Append(aS1); iMaterial = 1; aCBuilder.AddToResult (aLSToTake,aLSToAvoid, iMaterial); iMaterial = 2; aLSToAvoid.Clear(); aLSToTake.Clear(); aLSToTake.Append(aS2); aLSToAvoid.Append(aS1) aCBuilder.AddToResult (aLSToTake,aLSToAvoid, iMaterial); aLSToAvoid.Clear(); aLSToTake.Clear(); aLSToTake.Append(aS3); aLSToAvoid.Append(aS1) aCBuilder.AddToResult (aLSToTake,aLSToAvoid, iMaterial); DRAW: bcremoveall bcadd res s1 1 -m 1 bcadd res s2 1 s1 0 -m 2 bcadd res s3 1 s1 0 -m 2 bcremoveint res | 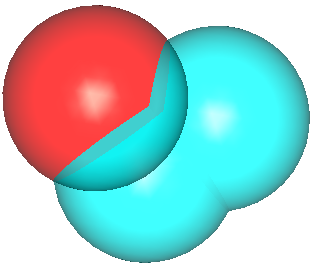 |
Note, that it is not needed to rebuild splits in order to build all these results. Once built, they are just reused for obtaining new results.
2. Multi-dimensional arguments
The following simple example demonstrates the possibilities of the algorithm on a box and an intersecting face. In this example we will perform the Boolean operations, which cannot be performed using the standard Boolean Operations algorithm. Input shapes:
box b 20 10 10 plane p 10 5 5 1 0 0 mkface f p -10 10 -10 10 bclearobjects bcleartools baddobjects b f bfillds bcbuild rx

Results:
| Example | Usage | Image of the result |
| Common operation | API: aLSToTake.Clear(); aLSToTake.Append(aBox); aLSToTake.Append(aFace); aLSToAvoid.Clear(); aCBuilder.AddToResult(aLSToTake,aLSToAvoid); DRAW: bcremoveall bcadd result b 1 f 1 |  |
| Fuse operation | API: aLSToTake.Clear(); aLSToTake.Append(aBox); aLSToAvoid.Clear(); aCBuilder.AddToResult(aLSToTake,aLSToAvoid, 1, Standard_True); aLSToTake.Clear(); aLSToTake.Append(aFace); aLSToAvoid.Clear(); aLSToAvoid.Append(aBox); aCBuilder.AddToResult(aLSToTake, aLSToAvoid); DRAW: bcremoveall bcadd result b 1 -m 1 -u bcadd result f 1 b 0 |  |
| CUT box from the face | API: aLSToTake.Clear(); aLSToTake.Append(aFace); aLSToAvoid.Clear(); aLSToAvoid.Append(aBox); aCBuilder.AddToResult(aLSToTake,aLSToAvoid); DRAW: bcremoveall bcadd result f 1 b 0 |  |
| CUT face from the box | API: aLSToTake.Clear(); aLSToTake.Append(aBox); aLSToAvoid.Clear(); aLSToAvoid.Append(aFace); aCBuilder.AddToResult(aLSToTake,aLSToAvoid); DRAW: bcremoveall bcadd result b 1 f 0 |  |
Again, the splits are built only once and just reused for building new results.
Tests on performance
The following environment has been used to measure the performance:
| Processor | Intel(R) Core(TM) i5-4460 CPU @ 3.20 GHz |
| System type | 64-bit Operating System |
| Installed memory (RAM) | 16GB |
| Operating System | Windows 10 Pro |
| Compiler | Microsoft Visual Studio Professional 2013, Version 12.0.31101.00 Update 4 |
| Open CASCADE | 7.1.0 development (master from 01/06/2017), optimized mode |
Since we use the same intersection part (Pave Filler) for BOPs and Cells Builder, only the performance of the building part will be measured. The set of 21x21 cylinders on a plate is used as a sample:
box b1 100 100 1
compound cylinders
for {set i 0} {$i < 101} {incr i 5} {
for {set j 0} {$j < 101} {incr j 5} {
pcylinder p 1 5;
ttranslate p $i $j -2;
add p cylinders;
}
}
bclearobjects; bcleartools
baddobjects b1
baddtools cylinders
bfillds

| Operations | Standard BOPs script | Cells Builder script | Standard BOPs, sec | Cells Builder, sec | Performance gain, times |
| CUT and then COMMON |
bbop r1 2 bbop r2 0 |
bcbuild rx bcremoveall bcadd r1 b1 1 cylinders 0 bcremoveall bcadd r2 b1 1 cylinders 1 |
3.46 | 1.93 | 1.79 |
| CUT and then FUSE |
bbop r1 2 bbop r2 1 |
bcbuild rx bcremoveall bcadd r1 b1 1 cylinders 0 bcremoveall bcaddall r2 -m 1 -u |
3.71 | 2.17 | 1.71 |
| CUT, COMMON and then opposite CUT |
bbop r1 2 bbop r2 0 bbop r3 3 |
bcbuild rx bcremoveall bcadd r1 b1 1 cylinders 0 bcremoveall bcadd r2 b1 1 cylinders 1 bcremoveall bcadd r3 b1 0 cylinders 1 |
5.6 | 1.93 | 2.9 |
Conclusion
The Cells Builder algorithm is a very useful and flexible tool for computing Boolean expressions on any number of shapes. It allows performing complex operations with minimal effort; it is just necessary to define the rules in terms of Cells - which ones to be taken and which to be excluded.

Wed, 07/05/2017 - 21:28
All the pictures are empty. Could you fix this problem to help understanding ?
TIA
Thu, 07/06/2017 - 08:53
Sorry for that. It's now fixed - the pictures have been added.
Thu, 07/06/2017 - 09:13
Thanks.
Fri, 10/23/2020 - 16:41
As we can see: In "CUT face from the box" the box now has two shapes. How can I access them independently?
Fri, 10/23/2020 - 16:49
They are not two shapes. It is one shape with internal face inside it.
Fri, 10/23/2020 - 16:54
Thanks for the response.
I am looking for a way to divide a shape into two (using a plane or face) and access them separately.
It would be great if you suggest any ideas.
Thanks in advance.
Fri, 10/23/2020 - 17:03
BRepAlgoAPI_Splitter does the thing.